Atcoderの記事だニャ

A問題

321や7531のように上の桁から数が小さくなっていく数字を321-like Numberとよびます。

3421や7533のような数は321-like Numberではありません。

Nが321-like Numberかどうか判定してください。

解答

Nを数字として入力すると少し複雑になるため、文字列として入力します。

Nがa桁だとします。

for文で1文字目からa文字目まで検証します。

i文字目がi+1文字目よりも大きければ次のループへ行き、そうでなければNoを出力してループから抜けます。

a文字目までループをしたらYesを出力します。

N = input()

for i in range(len(N)):
    if i == len(N)-1:
        print('Yes')
        break

    if int(N[i]) <= int(N[i+1]):
        print('No')
        break

B問題

Nラウンドからなる試験があります。

各ラウンドで0点から100点のスコアが与えられます。

Nラウンドのスコアのうち最高スコアと最低スコアを除いたN-2ラウンドの合計が総合スコアです。

N-1ラウンドまでのスコアが与えられているとき、Nラウンド目に最低で何点獲得すると総合スコアがXに到達しますか。

解答

まず、最低スコアと最高スコアを把握するためにスコアを小さい順に並べ替えます。

並べ替えるにはsort()を使います。

sort関数はもとのリストを書き換えてしまいますが、今回はそれで問題は起きません。

気になる人はsorted()で新しいリストを使いましょう。

3つにパターン分けをして考えました。

①最高スコアを抜いた合計スコアがXに到達するパターン

最高スコア以外ですでにXに到達しているのでNラウンド目は0点でOK。

②Xに到達するまでの残りスコアが最低スコア以上、最高スコア以下のパターン

Nラウンド目に残りスコア分獲得すればOK。

最低スコア以上、最高スコア以下なのでNラウンド目のスコアを含めてXに到達します。

③Xに到達するまでの残りスコアが最高スコア以上のパターン

Nラウンド目に最高スコア以上の得点を獲得しても総合スコアに反映されません。

したがって、総合スコアがXを超えることは不可能です。

無理な場合には-1を出力します。

これでOKだと思いましたが、N=3のときにスライス(A[1:-1])でバグるので別で処理しました。

N, X = map(int, input().split())
A = list(map(int, input().split()))

A.sort()

if N == 3:
    if A[0] >= X:
        print(0)
    elif A[0] <= X <= A[1]:
        print(X)
    else:
        print(-1)

elif sum(A[0:-1]) >= X:
    print(0)

elif A[0] <= X - sum(A[1:-1]) <= A[-1]:
    print(X - sum(A[1:-1]))

else:
    print(-1)

公式の解説では0点の場合から100点の場合までを全探索していました。

確かに最大101ループなのでその方法の方が短いコードで済みそうですね。

C問題

A問題と似ています。

正の整数Kが与えられます。

K番目に小さい321-like Numberを出力してください。

解答

321-like Numberの特徴として、同じ数字は出てこないです。

例えば97443は321-like Numberではないです。

したがって321-like Numberは最大10桁の数であることが分かります。

また、最大の321-like Numberは9876543210であることが分かりました。

この考察から次のように考えることができます。

①0~9の数のそれぞれを1度ずつ使うか使わないかを選ぶことができる。

②使った数字を大きい順に並べると321-like Numberになる。

例えば0~9のうち0、2、6、8、9を1度ずつ選ぶとします。

これを大きい順に並べると98620となり、これは321-like Numberです。

これをpythonでどのように実装するかというと、bit全探索を行います。

bit全探索はPython de アルゴリズム（bit全探索）のサイトが分かりやすいです。

選べる数字は10種類なので2¹⁰通りのパターンがあります。

for文で2¹⁰回ループしてすべての321-like Numberをリストに格納します。

for文で何が行われているかは次の画像と先ほど紹介したページを見てもらえれば分かると思います。

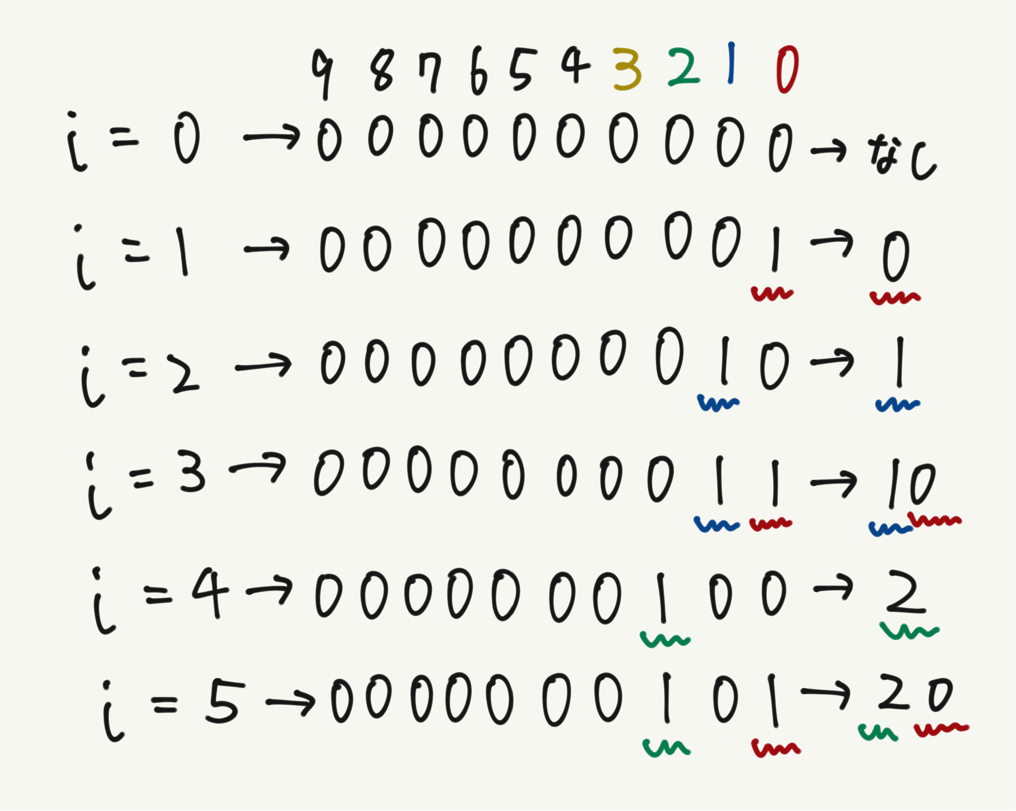
簡単に説明するとfor文で2¹⁰回ループするとiは0~1023の値をとります。

iを2進数に変換すると最大10桁の数となります。

1桁ごとに0~9の数字と対応していると考えます。

2進数で0の桁は対応する数字を使わず、1なら対応する数字を使うというコードを組みます。

この321-like Numberは小さい順になってないので、sort関数で並べ替えます。

最後にi=0,1のときは両方0となるので、これらを除外するためにl[K+1]として補正します。

K = int(input())
l = []

for i in range(2**10):
    l2 = []
    num = 0

    for j in range(10):
        if (i >> j) & 1:
            l2.append(j)

    for k in range(len(l2)):
        num += l2[k] * 10**k
    l.append(num)

l.sort()

print(l[K+1])